ESTALMAT CV
19 de septiembre de 2011
COMIENZA EL CURSO ESTALMAT CV 2011-2012
El 1 de octubre comenzará el campamento en Requena, y el día 8, la conferencia inaugural estará a cargo de Antonio Ledesma, que hablará sobre poesía visual.
ESTALMAT CV
ESTALMAT CV
ESPECIALMENTE PARA Mª JOSÉ
Estos últimos días he estado recortando y haciendo pruebas con esto:
http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2003/EricBiunno/
En realidad el origen de mi curiosidad se debe a un documental que vi con mi hermana Cristina este verano sobre papiroflexia. El documental pretendía dar una visión amplia y global sobre todas las vertientes del origami. La parte tradicional japonesa, sus orígenes, la parte artística, la matemática... Y apareció este teorema, que en castellano le llamaban "del corte único" o algo así.
Yo he hecho pruebas con esta imágen:
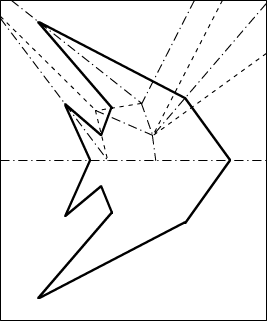
Y sale bien. Pero me interesaba más saber como se hacía sin que hubiera que dibujar las líneas. Y entonces, consultando la página del superdotado que había demostrado este teorema, http://erikdemaine.org/foldcut/, encuentro la historia de Betsy Ross.
Pero más alucinante aun me pareció este vídeo:
Así que con mis alumnos de 1º me dediqué el otro día a cortar corazoncitos. Muy difícil para ellos, pero me sirvió para detectar las grandes carencias que tienen en conocimientos de Geometría. ¡No saben reconocer un cuadrado!
Bueno, espero que te haya gustado y que te proporcione algunos ratitos de entretenimiento.
http://cgm.cs.mcgill.ca/~athens/cs507/Projects/2003/EricBiunno/
En realidad el origen de mi curiosidad se debe a un documental que vi con mi hermana Cristina este verano sobre papiroflexia. El documental pretendía dar una visión amplia y global sobre todas las vertientes del origami. La parte tradicional japonesa, sus orígenes, la parte artística, la matemática... Y apareció este teorema, que en castellano le llamaban "del corte único" o algo así.
Yo he hecho pruebas con esta imágen:
Y sale bien. Pero me interesaba más saber como se hacía sin que hubiera que dibujar las líneas. Y entonces, consultando la página del superdotado que había demostrado este teorema, http://erikdemaine.org/foldcut/, encuentro la historia de Betsy Ross.
Pero más alucinante aun me pareció este vídeo:
Así que con mis alumnos de 1º me dediqué el otro día a cortar corazoncitos. Muy difícil para ellos, pero me sirvió para detectar las grandes carencias que tienen en conocimientos de Geometría. ¡No saben reconocer un cuadrado!
Bueno, espero que te haya gustado y que te proporcione algunos ratitos de entretenimiento.
FUTBOL Y MATEMÁTICAS
Juan Mata presenta este desafío sobre equipos y jugadores
Otros desafíos anteriores los podéis encontrar en estos enlaces:
Alfombras triangulares
http://www.elpais.com:80/videos/sociedad/alfombras/triangulares/elpepusoc/20110901elpepusoc_2/Ves/
Solución
http://www.elpais.com:80/videos/sociedad/Areas/equivalentes/elpepusoc/20110906elpepusoc_1/Ves/
Construyendo superficies
http://www.elpais.com:80/videos/sociedad/Construyendo/superficies/elpepusoc/20110908elpepusoc_4/Ves/
Solución
http://www.elpais.com/articulo/sociedad/flotador/biplaza/elpepusoc/20110913elpepusoc_13/Tes
Otros desafíos anteriores los podéis encontrar en estos enlaces:
Alfombras triangulares
http://www.elpais.com:80/videos/sociedad/alfombras/triangulares/elpepusoc/20110901elpepusoc_2/Ves/
Solución
http://www.elpais.com:80/videos/sociedad/Areas/equivalentes/elpepusoc/20110906elpepusoc_1/Ves/
Construyendo superficies
http://www.elpais.com:80/videos/sociedad/Construyendo/superficies/elpepusoc/20110908elpepusoc_4/Ves/
Solución
http://www.elpais.com/articulo/sociedad/flotador/biplaza/elpepusoc/20110913elpepusoc_13/Tes
Suscribirse a:
Entradas (Atom)